787. Cheapest Flights Within K Stops (Python)

Related Topic

Breadth-First-Search. Dijkstra. Graph.

Description

There are n cities connected by m flights. Each flight starts from city u and arrives at v with a price w.

Now given all the cities and flights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.

Sample I/O

Example 1

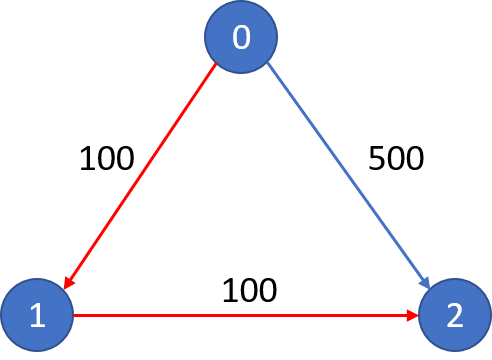
Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200
Explanation: 
The graph looks like above:
The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.

Example 2

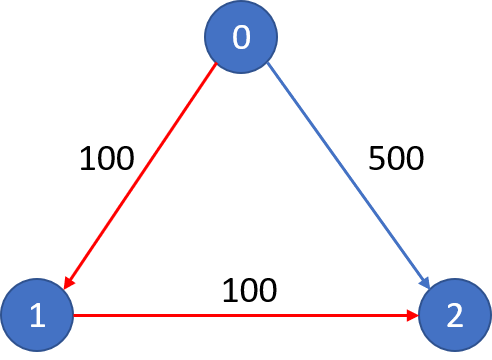
Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
Output: 500
Explanation: 
The graph looks like above:
The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.

Constrains

• The number of nodes n will be in range [1, 100], with nodes labeled from 0 to n - 1.
• The size of flights will be in range [0, n * (n - 1) / 2].
• The format of each flight will be (src, dst, price).
• The price of each flight will be in the range [1, 10000].
• k is in the range of [0, n - 1].
• There will not be any duplicated flights or self cycles.

Methodology

This is a graph question. We can solve it either by using BFS or Dijkstra.

BFS:

For each flight there are starting city, destination and cost. We will store it into dictionary with key is the starting city and value is another dictionary that contain destnation and cost pair. We also need a queue to implement the flight routes. The queue include starting city and cost (init to 0) initially. Now we pop the queue if the current starting city is destination then we find the smaller cost and update the cost. Otherwise we need to find the next station and cost in graph based on the current station. We append the next station and total cost into queue continuely until the queue is empty then we return the min cost.

Dijkstra:

Dijkstra is similar with BFS, the difference is using priority queue instand of queue. The priority will always pop the element with heigher priority. In this case, the cost is lower the priority is heigher. Once the pop src is equal to destination we will have the answer.

BFS:

def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
        graph=collections.defaultdict(dict)
        for u,v,w in flights:
            graph[u][v]=w
        queue = collections.deque([(src,0)])
        ans, step = float('inf'), 0
        while queue:
            for _ in range(len(queue)):
                cur,cost = queue.popleft()
                if cur == dst:
                    ans=min(ans,cost)
                    continue
                for v,w in graph[cur].items():
                    if cost + w>ans:
                        continue
                    queue.append((v,cost+w))
            if step > K: break
            step+=1
        return -1 if ans == float('inf') else ans

BigO

Time complexity : O(E*K) where E is the number of edges and K is the number of stops given

Dijkstra:

def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
        pq,graph=[(0, src, 0)],collections.defaultdict(dict)
        for u,v,w in flights:
            graph[u][v]=w
        while pq:
            total, src, stops = heapq.heappop(pq)
            if src == dst: return total
            if stops > K: continue
            for dest, cost in graph[src].items():
                heapq.heappush(pq,(total+cost, dest, stops+1))
        return -1

BigO

Time Complexity: Let EE represent the number of flights and VV represent the number of cities. The time complexity is mainly governed by the number of times we pop and push into the heap. We will process each node (city) atleast once and for each city popped from the queue, we iterate over its adjacency matrix and can potentially add all its neighbors to the heap. Thus, the time taken for extract min and then addition to the heap (or simply, heap replace) would be \text{O}(\text{V}^2 \cdot \text{log V})O(V 2 ⋅log V).