173. Binary Search Tree Iterator (Python)

Related Topic

Stack.

Description

Implement an iterator over a binary search tree (BST). Your iterator will be initialized with the root node of a BST.

Calling next() will return the next smallest number in the BST.

Sample I/O

Example 1

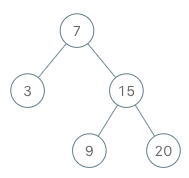
BSTIterator iterator = new BSTIterator(root);
iterator.next();    // return 3
iterator.next();    // return 7
iterator.hasNext(); // return true
iterator.next();    // return 9
iterator.hasNext(); // return true
iterator.next();    // return 15
iterator.hasNext(); // return true
iterator.next();    // return 20
iterator.hasNext(); // return false

Methodology

The binary search has one important properity that is left node value is smaller than root value and right node value is greater than root value. You can use the brutal force method that each time call next you will traversal the tree and find the smallest node then remove it from tree recusively. This is not efficient. To better solve this question, you can try to use stack and preorder traversal (Root, Left, Right) to append the left node value into stack. Once you call next, you pop the top of the stack. This will always return the smallest value from stack due to the property of BST. Then you append the right node the the poped node if it is existed because the right node is always greater than root and smaller than the root’s parent.

class BSTIterator:

    def __init__(self, root: TreeNode):
        self.stack = []
        self.push_left(root)
        

    def next(self) -> int:
        """
        @return the next smallest number
        """
        node = self.stack.pop()
        self.push_left(node.right)
        return node.val

    def hasNext(self) -> bool:
        """
        @return whether we have a next smallest number
        """
        return self.stack
        
    def push_left(self, root):
        while root:
            self.stack.append(root)
            root = root.left

BigO

Iterate the tree will cost O(n) and iterate the stack will cost O(n). In total will be O(2n)