142. Linked List Cycle II (Python)

Related Topic

Linked-List. Two-Pointers.

Description

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Note

Do not modify the linked list.

Sample I/O

Example 1

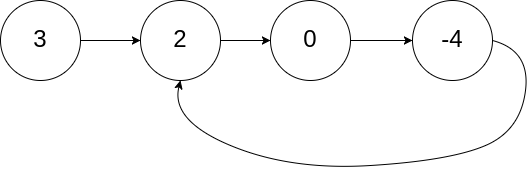
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2

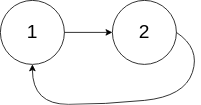
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Follow Up

Can you solve it without using extra space?

Methodology

This is the extension quesion of 141. Linked List Cycle Now we want to return the start node of cycle

1. We need to check if there is cycle
2. If there is not cycle return None and if there is cycle we set slow pointer to head
3. If slow pointer and fast pointer are not equal we move 1 step for each pointer until the two pointer conincide, then we get the node of cycle begining.

There are lots of explainations online, the best way to try is draw graph yourself. There is simple math behind. Here

• L1: the distance from head to start node of cycle
• L2: the distance from start node of cycle to crossing node of two pointers
• L3: the distance from crossing node of two pointers to start node of cycle

Slow pointer to crossing node is L1+L2.

Fast pointer to crossing node is 2(L1+L2) since fast pointer always move 2 times of slow pointer step.

Fast pointer is also equal to L1+L2+L3+L2 because to meet with slow pointer, the fast pointer has to run over cycle at least 1 time.

Therefor 2(L1+L2)=L1+L2+L3+L2 -> 2L1=L1+L3 -> L1 = L3

Code

def detectCycle(self, head: ListNode) -> ListNode:
        slow, fast = head, head
        while fast and fast.next:
            fast = fast.next.next
            slow = slow.next
            if fast == slow:
                break
        if not fast or not fast.next:
            return None
        slow = head
        while slow != fast:
            slow = slow.next
            fast = fast.next
        return fast

BigO

Iterate the both linked lists once, so total time complexity is O(m+n) where m steps of fast pointer and n is steps of slow pointer