909. Snakes and Ladders (Python)

Related Topic

Breadth-First-Search.

Description

On an N x N board, the numbers from 1 to N*N are written boustrophedonically starting from the bottom left of the board, and alternating direction each row. For example, for a 6 x 6 board, the numbers are written as follows:

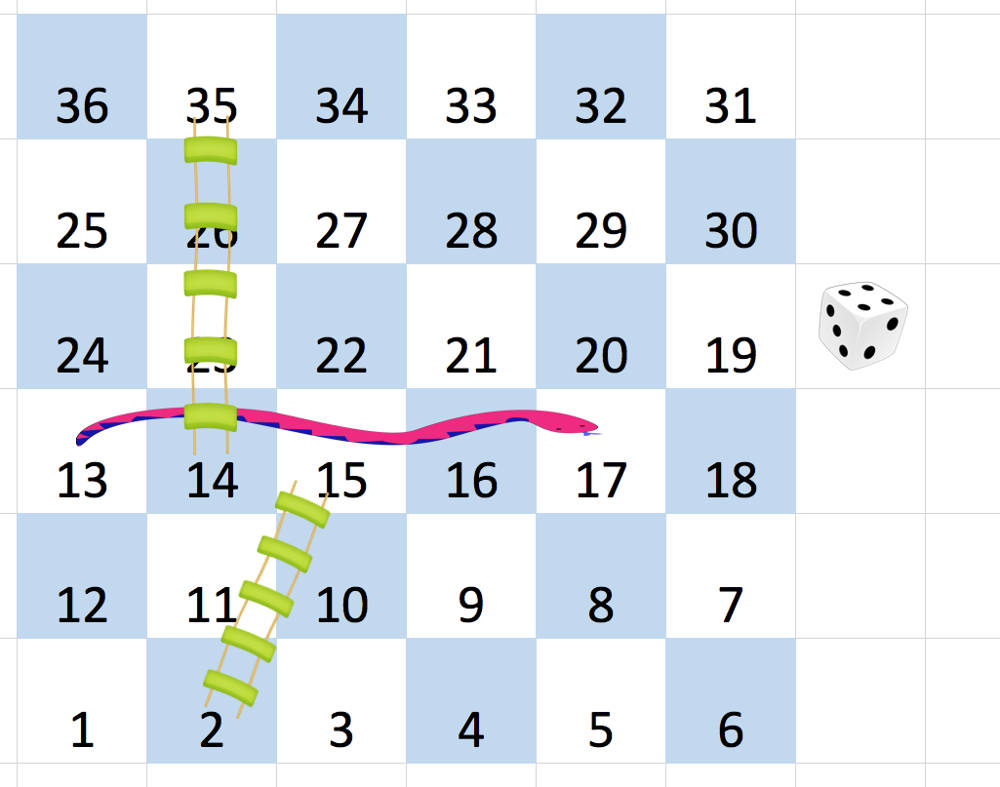
You start on square 1 of the board (which is always in the last row and first column). Each move, starting from square x, consists of the following:

• You choose a destination square S with number x+1, x+2, x+3, x+4, x+5, or x+6, provided this number is <= N*N.
  • (This choice simulates the result of a standard 6-sided die roll: ie., there are always at most 6 destinations, regardless of the size of the board.)
• If S has a snake or ladder, you move to the destination of that snake or ladder. Otherwise, you move to S. A board square on row r and column c has a “snake or ladder” if board[r][c] != -1. The destination of that snake or ladder is board[r][c].

Note that you only take a snake or ladder at most once per move: if the destination to a snake or ladder is the start of another snake or ladder, you do not continue moving. (For example, if the board is [[4,-1],[-1,3]], and on the first move your destination square is 2, then you finish your first move at 3, because you do not continue moving to 4.)

Return the least number of moves required to reach square N*N. If it is not possible, return -1.

Sample I/O

Example 1

Input: [
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,35,-1,-1,13,-1],
[-1,-1,-1,-1,-1,-1],
[-1,15,-1,-1,-1,-1]]
Output: 4
Explanation: 
At the beginning, you start at square 1 [at row 5, column 0].
You decide to move to square 2, and must take the ladder to square 15.
You then decide to move to square 17 (row 3, column 5), and must take the snake to square 13.
You then decide to move to square 14, and must take the ladder to square 35.
You then decide to move to square 36, ending the game.
It can be shown that you need at least 4 moves to reach the N*N-th square, so the answer is 4.

Note

• 2 <= board.length = board[0].length <= 20
• board[i][j] is between 1 and N*N or is equal to -1.
• The board square with number 1 has no snake or ladder.
• The board square with number N*N has no snake or ladder.

Methodology

Start from the first square and get the location of the square. If the next square is snake or ladders, jump to the indicated square and increase 1 unit of step from current square. Then store the square and step into dictionary. If the next square is a normal square, then we just increase 1 unit of step from current and store the square and step pair into dictionary. Finally if the square is last suqare we return the step.

Note tha to find the location of square. We need to know the current square in odd row or even row. If in odd row, location will start from left to right. If in even row, location will start from right to left. We count row from top to bottom and start from row 0.

Code (BFS)

def snakesAndLadders(self, board: List[List[int]]) -> int:
        rows = len(board)
        total_square = rows*rows

        def next_square(step):
            quot, rem = divmod(step-1, rows)
            row = (rows - 1) - quot
            if row%2 != rows%2:
                col = rem 
            else:
                col = (rows - 1) - rem
            return row, col

        dist = {1: 0}#square and step
        queue = collections.deque([1])
        while queue:
            square = queue.popleft()
            if square == total_square:
                return dist[square]
            for new_square in range(square+1, min(square+6, total_square) + 1):
                r, c = next_square(new_square)
                if board[r][c] != -1:
                    new_square = board[r][c]
                if new_square not in dist:
                    dist[new_square] = dist[square] + 1
                    queue.append(new_square)
        return -1

BigO

We traversal all elements of 2D list once so total time complexity is O(n) where is the size of the 2D list