1091. Shortest Path in Binary Matrix (Python)

Related Topic

Breadth-First-Search.

Description

In an N by N square grid, each cell is either empty (0) or blocked (1).

A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, …, C_k such that:

• Adjacent cells C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)
• C_1 is at location (0, 0) (ie. has value grid[0][0])
• C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])
• If C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0). Return the length of the shortest such clear path from top-left to bottom-right. If such a path does not exist, return -1.

Sample I/O

Example 1

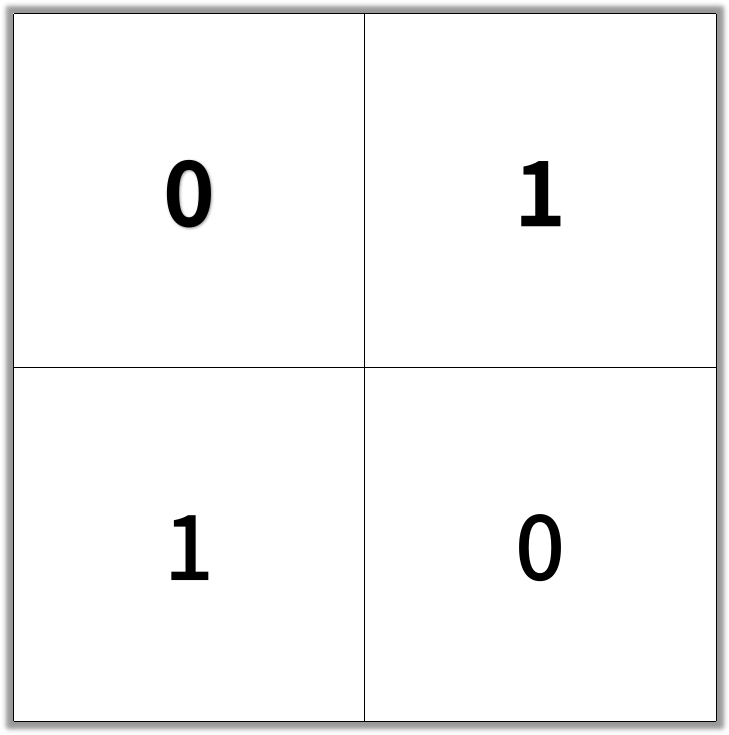
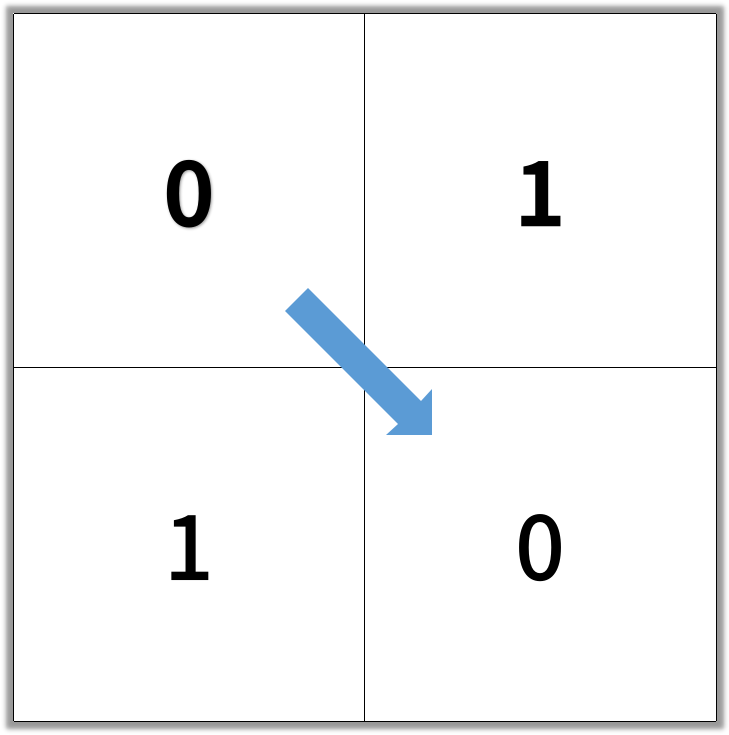
Example 2

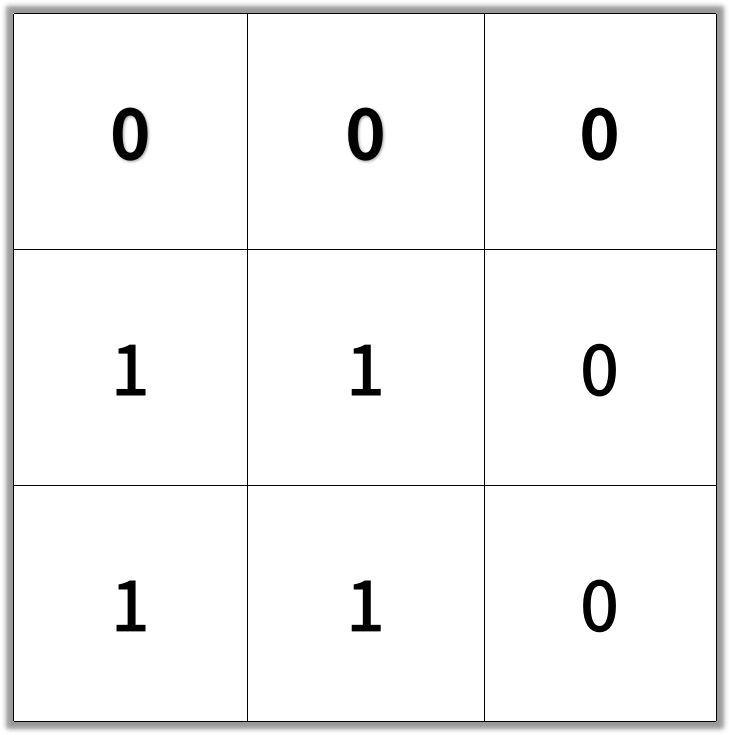
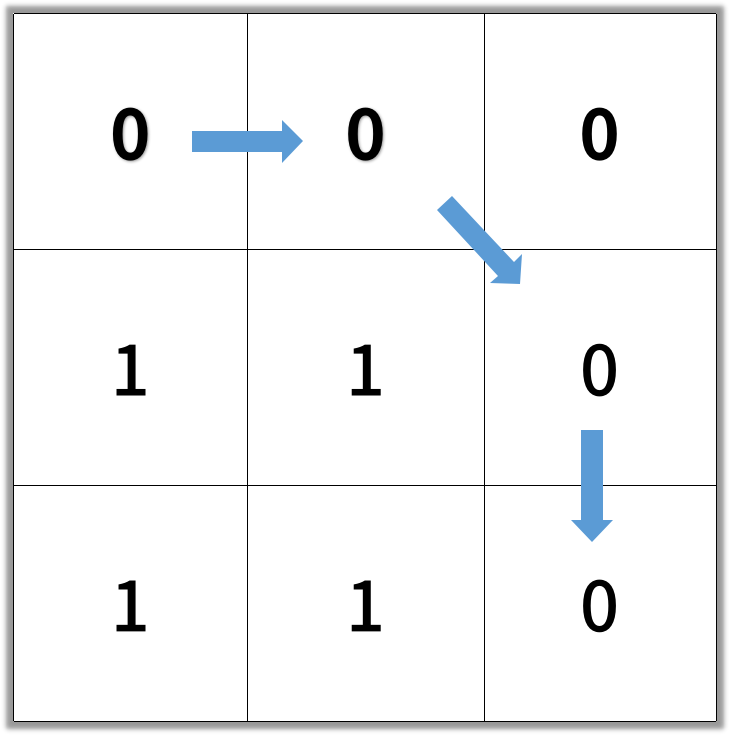
Note

• 1 <= grid.length == grid[0].length <= 100
• grid[r][c] is 0 or 1

Methodology

Append the start path coordinate to queue. Use BFS traversal the 2D list from path coordinate pop out from queue. Each time expand the current path coordinate for 8 directions. And append the 8 directions’s path to queue. The first path to reach bottom right will return the steps.

Code (BFS)

def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
        dirs = [(-1,-1),(-1,0),(-1,1),(0,1),(1,1),(1,0),(1,-1),(0,-1)]
        row,col = len(grid),len(grid[0])
        if grid[0][0] or grid[-1][-1]:
            return -1
        if row == 1 and grid[0][0] == 0:
            return 1
        q = collections.deque()
        q.append((0,0))
        visited = set()
        visited.add((0,0))
        step = 1
        while q:
            for _ in range(len(q)):
                x, y = q.popleft()
                for dx, dy in dirs:
                    nx, ny = x+dx, y+dy
                    if 0 <= nx< row and 0<= ny < col and grid[nx][ny] == 0 and (nx,ny) not in visited:
                        visited.add((nx,ny))
                        q.append((nx,ny))
                        if nx == row-1 and ny == col-1:
                            return step + 1
            step += 1
        return -1

BigO

We traversal all elements of 2D list once so total time complexity is O(mn) where m is the size of row and n is the size of column