Leetcode 505. The Maze II (Python)

Related Topic

Breadth-First-Search.

Description

There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won’t stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the ball’s start position, the destination and the maze, find the shortest distance for the ball to stop at the destination. The distance is defined by the number of empty spaces traveled by the ball from the start position (excluded) to the destination (included). If the ball cannot stop at the destination, return -1.

The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.

Sample I/O

Example 1

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)

Output: 12

Explanation: One shortest way is : left -> down -> left -> down -> right -> down -> right.The total distance is 1 + 1 + 3 + 1 + 2 + 2 + 2 = 12.

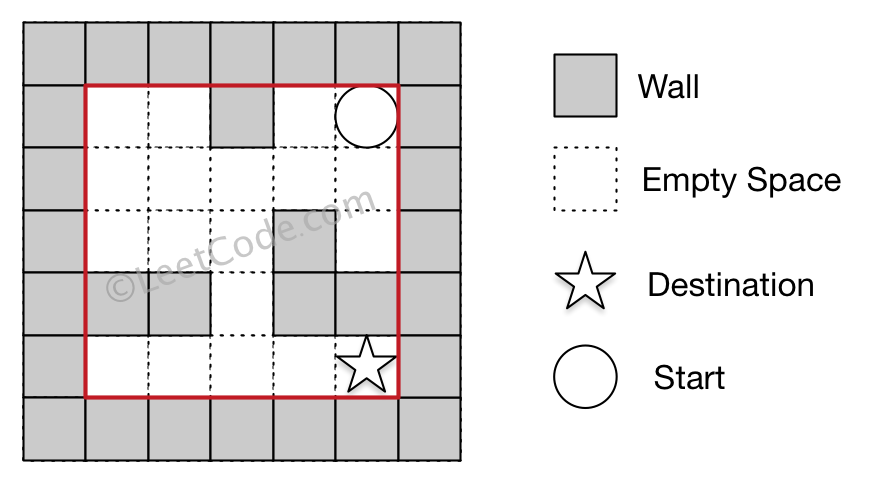
Example 2

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)

Output: -1

Explanation: There is no way for the ball to stop at the destination.

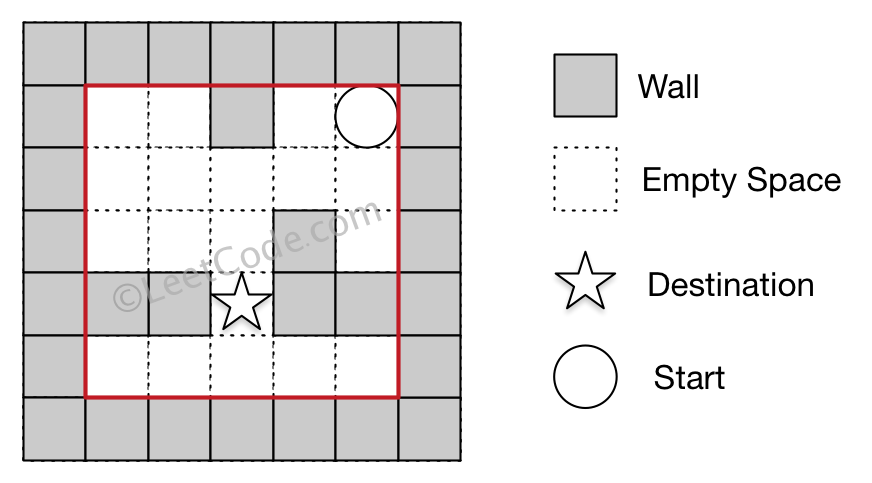
Note:

1. There is only one ball and one destination in the maze.
2. Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
3. The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
4. The maze contains at least 2 empty spaces, and both the width and height of the maze won’t exceed 100.

Methodology

The question is extended from 490. The Maze . This time ask to get shortest distance.

Same method to get the end point plus need to record the distance. We use heap because heapq because when we need to pop from heapq, it will automaticlly pop the minimum value.

Code(DFS+BFS)

def shortestDistance(self, maze: List[List[int]], start: List[int], destination: List[int]) -> int:      
        start, destination = tuple(start), tuple(destination)
        row,col = len(maze),len(maze[0])
        def neighbors(maze, node):
            temp = []
            used = set()
            used.add(node)
            for dx, dy in [(-1, 0), (0, 1), (0, -1), (1, 0)]:
                (x,y), dist = node, 0
                while 0 <= x+dx < row and 0 <= y+dy < col and maze[x+dx][y+dy] == 0:
                    x += dx
                    y += dy
                    dist += 1
                if (x,y) not in used:
                    temp.append((dist, (x,y)))
            return temp

        heap = [(0, start)]
        visited = set()
        while heap:
            dist, node = heapq.heappop(heap)
            if node in visited: continue
            if node == destination:
                return dist
            visited.add(node)
            for neighbor_dist, neighbor in neighbors(maze, node):
                heapq.heappush(heap, (dist+neighbor_dist, neighbor))
        return -1

BigO

We traversal all elements of the 2D roughly once so time complexity is roughly O(mn) where m is row size and n is column size.