杰弗里 · 时光博客(Jeffrey's Blog)

leetcode 979. Distribute Coins in Binary Treet (Python)

14 Mar 2020 Leetcode Depth-First-Search Tree Postorder-Traversal Inorder-Traversal

Leetcode 979. Distribute Coins in Binary Tree (Python)

Related Topic

Depth-First-Search. Tree. Postorder-Traversal.

Description

Given the root of a binary tree with N nodes, each node in the tree has node.val coins, and there are N coins total.

In one move, we may choose two adjacent nodes and move one coin from one node to another. (The move may be from parent to child, or from child to parent.)

Return the number of moves required to make every node have exactly one coin.

Sample I/O

Example 1

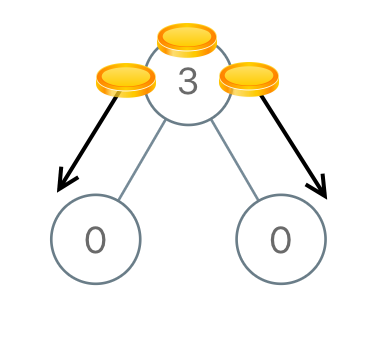
tree1

Input: [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2

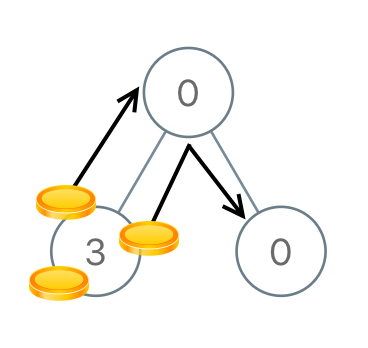
tree2

Input: [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves].  Then, we move one coin from the root of the tree to the right child.

Example 3

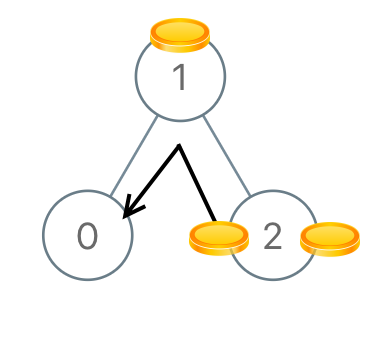
tree3

Input: [1,0,2]
Output: 2

Example 4

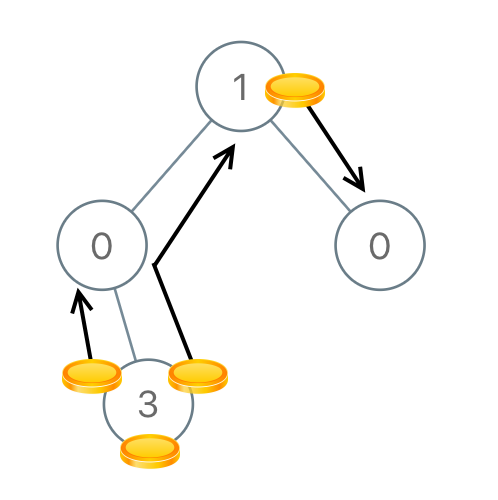
tree4

Input: [1,0,0,null,3]
Output: 4

Note

  • 1<= N <= 100
  • 0 <= node.val <= N

Methodology

This question can be solved by Depth First Search.

To make all tree nodes have exactly 1 coin. We will use DFS to find excess or shortage number of coins in subtree. For example, if the total coins of a subtree, which include root, left edge and right edge, should have 3 coins in total but you got 4 coins, then this subtree must give 1 coin to it’s parent tree. If the subtree should have 5 coins and it only have 3 coins, then it will need parent tree give it 2 coins. Note, no matter, it give coins to parent or it accept coins from parent. This procee will need positive number of moves.

This question make me have deeper understand of recursion, it is a great one.

Code

def distributeCoins(self, root: TreeNode) -> int:
        def dfs(root, result):
            if not root:
                return 0
            left_edge = dfs(root.left, result) 
            right_edge = dfs(root.right, result)
            result[0] += abs(left_edge) + abs(right_edge)
            return root.val + left_edge + right_edge - 1

        result = [0]
        dfs(root, result)
        return result[0]

BigO

We traversal all nodes once so the total time complexity is O(n)

Search

    Table of Contents