Leetcode 117. Populating Next Right Pointers in Each Node II (Python)

Related Topic

Breadth-First-Search. Tree.

Description

Given a binary tree

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

• You may only use constant extra space.
• Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Sample I/O

Example 1

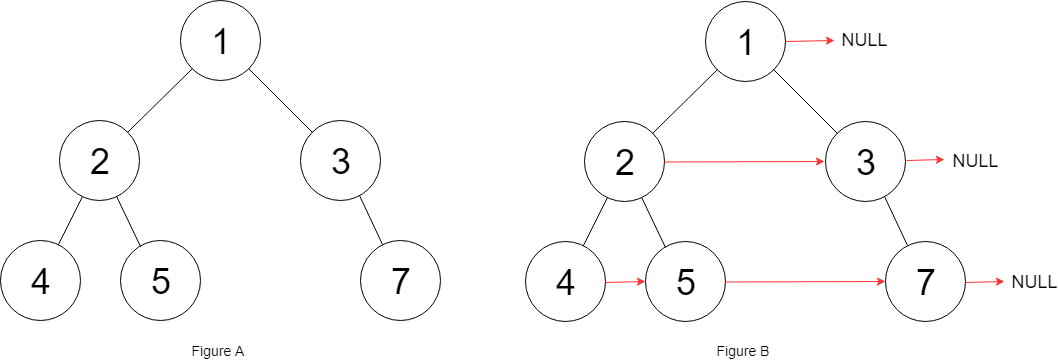
Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Constraints

• The number of nodes in the given tree is less than 6000.
• -100 <= node.val <= 100

Methodology

This question can be solved by Breadth First Search. It is similar with question 116. Populating Next Right Pointers in Each Node . The difference is the tree is no longer perfect binary tree.

To point all nodes to their next right node. We are going to use BFS. We need go through each level. In each level, we will get all nodes from left to right and use next pointer to connect each other.

Code

"""
# Definition for a Node.
class Node:
    def __init__(self, val, left, right, next):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""
class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if not root:
            return root
        Q = collections.deque([root])
        while Q:
            size = len(Q)
            for i in range(size):
                node=Q.popleft()
                if i<size-1:
                    node.next=Q[0]
                if node.left:
                    Q.append(node.left)
                if node.right:
                    Q.append(node.right)
        return root

BigO

We traversal all nodes of the tree once so the time complexity is O(n)