Leetcode 62. Unique Paths (Python)

Related Topic

Dynamic-Programming.

Description

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

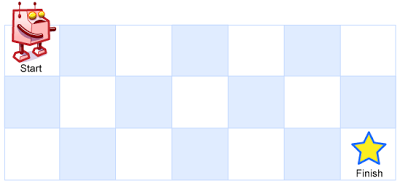
Sample I/O

Example 1

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2

Input: m = 7, n = 3
Output: 28

Note:

m and n will be at most 100.

Methodology

This question solved by Dynamic Programming.

1. Find the base case:

   There is only one way to reach the left most edge and there is only one way to reach the bottom most edge. So we init the first row and first column of 2D list with 1.

   1,1,1,1,1,1,1
   1,x,x,x,x,x,x
   1,x,x,x,x,x,x
   1,x,x,x,x,x,x
   

   ….

2. Find the pattern:

   The robot can only move either down or right. For each target cell that the robot want to reach, it is either from left cell of the tagret or from up cell of the target. Therefor we need sum up target’s left cell and up cell to get the total path to reach the target cell.

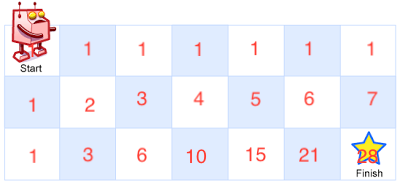
3. Answer:

   When reach to the bottom-right corner, then number in the bottom-right corner will be the answer.

Code

def uniquePaths(self, m: int, n: int) -> int:
        dp = [[0]*n for _ in range(m)]
        for i in range(m):
            dp[i][0] = 1
        for j in range(n):
            dp[0][j] = 1
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j] = dp[i-1][j]+dp[i][j-1]
        return dp[m-1][n-1]

BigO

Init the first row and first column that will cost O(m+n). Then iterate all 2D dp array, it will cost O(m*n). In total will cost (m+n+mn), So generally, it is O(n^2)